Ctrl+K

Convergence (Quantitative)

Convergence (Quantitative)#

Requirements

  • Complete the Telemac steady 2d tutorial (or similar).

  • The MASS-BALANCE : YES and/or PRINTING CUMULATED FLOWRATES : YES keywords must have been used in the steering (.cas) file to print mass fluxes across liquid boundaries in the Terminal.

  • The Telemac simulation must have been running with the s flag (more details below):

telemac2d.py [STUDY-NAME].cas -s

All required simulation files for this tutorial can be downloaded from the hydro-informatics/telemac repository on GitHub (see details below).

Goals & purpose

This tutorial describes the verification of flux convergence to optimize the required number of simulation timesteps (NUMBER OF TIME STEPS) of a steady Telemac simulation. Such convergence analysis is recommended before using steady simulation results for hotstarting an unsteady or a morphodynamic (sediment transport) simulation. However, the here-shown scripts can also serve for comparison of travel times of flood waves traveling from an upstream to a downstream boundary.

If you are looking for solutions to fix a non-converging model, please refer to the spotlight chapter on mass conservation and make sure the liquid boundaries are well defined.

This chapter uses the simulation files from the Telemac steady 2d tutorial, but with a slightly different definition of timesteps and printout periods:

/ steady2d-conv.cas
TIME STEP : 1.
NUMBER OF TIME STEPS : 10000
GRAPHIC PRINTOUT PERIOD : 50
LISTING PRINTOUT PERIOD : 50

Additionally, the simulation was rerun with the -s flag, which saves the simulation state in a file called similar to [FILE-NAME].cas_YEAR-MM-DD-HHhMMminSSs.sortie.

telemac2d.py steady2d-conv.cas -s

Both the steering .cas and .sortie files can be downloaded from the hydro-informatics.com repositories:

Extract and Check Flux Data#

Alternative: use control sections

This section features flux (flow) convergence analysis directly from Telemac message logging with Python. Alternatively, fluxes can be extracted by defining control sections (read more in the unsteady tutorial.

The Telemac jupyter notebook templates (HOMETEL/notebooks/ > data_manip/extraction/*.ipynb or workshops/exo_fluxes.ipynb) provide some guidance for extracting data from simulation results, which can be tweaked into a generally applicable framework for observing mass convergence at the boundaries as a function of the defined NUMBER OF TIME STEPS. However, the notebook templates do not work straightforwardly, which is why the following paragraphs describe a simple, minimalist Python tweak called pythomac, developed by hydro-informatics.com. There are three options for working with our codes, and all of them require having an installation of Python along with the numpy, pandas, and matplotlib libraries (see the Python installation guide):

Pip-install the pythomac package:

pip install pythomac

Clone the pythomac repository from GitHub:

git clone https://github.com/hydro-informatics/pythomac.git

Copy-paste the folder pythomac/pythomac/ into your simulation directory. That is, make sure that the Python script /HOME/pythomac/extract_fluxes.py (among others) is correctly located, next to /HOME/your-simulation-dir/steady2d.cas.

Download a zipped archive of the pythomac repository from GitHub (right-click here > save as…). Open the zip archive > open pythomac-main, and extract the contents of the pythomac folder (i.e., pythomac-main/pythomac/) next to your simulation directory. That is, make sure that the Python script /HOME/pythomac/extract_fluxes.py (among others) is correctly located, next to /HOME/your-simulation-dir/steady2d.cas.

Detailed instructions for using the extract_fluxes() function through pythomac and its dependencies (numpy, pandas, and matplotlib) can be found at https://pythomac.readthedocs.io.

To use the functions defined in pythomac, copy the following code into a new Python script called, for instance, example_flux_convergence.py in the directory where the dry-initialized steady2d simulation ran (or download example_flux_convergence.py):

# example_flux_convergence.py

from pathlib import Path
from pythomac import extract_fluxes

simulation_dir = str(Path(__file__).parents[1])
telemac_cas = "steady2d.cas"

fluxes_df = extract_fluxes(
    model_directory=simulation_dir,
    cas_name=telemac_cas,
    plotting=True
)

Got errors? Verify that the simulation directories are correct.

Adding a simple print(simulation_dir) line in the above code block might help to check the correctness of directories. That is, the Python code should be able to fine the simulation.

Run the Python script from Terminal (or Anaconda Prompt) as follows (make sure to cd into the simulation directory):

python example_flux_convergence.py

The script will have placed in the simulation folder:

  • a CSV file called extracted_fluxes.csv (download), and

  • a plot of flux convergences (flux-convergence.png) across the model boundaries (see Fig. 198) showing qualitatively that the fluxes reached convergence after approximately 6000-7000 timesteps.

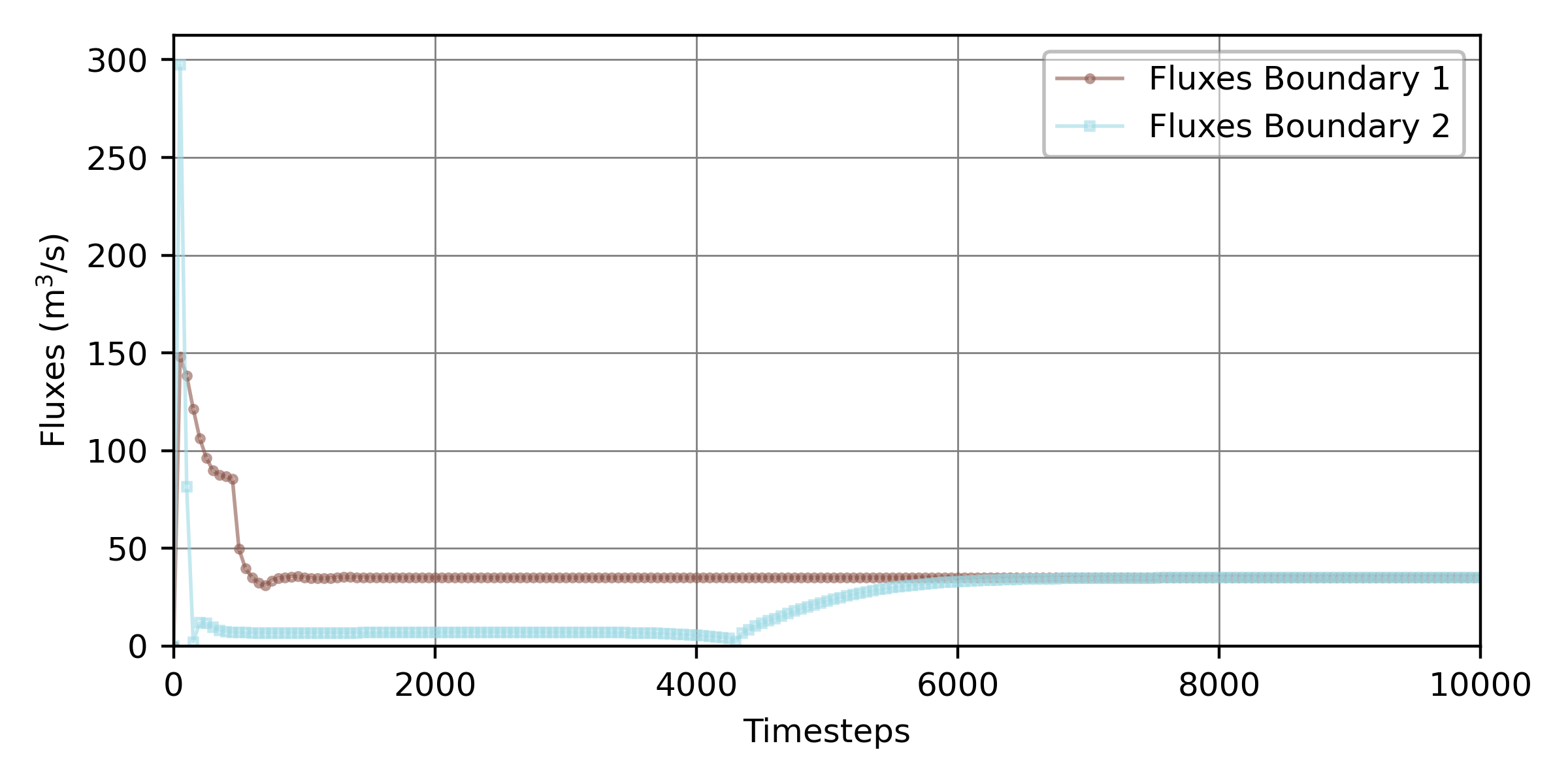
python telemac flux discharge convergence pythomac

Fig. 198 Flux convergence plot across the two boundaries of the dry-initialized steady Telemac2d simulation with a total simulation time of timesteps seconds, created with the pythomac.extract_fluxes() function.#

Identify Convergence#

To test if and when the fluxes converged, we can calculate the differences between fluxes for every timestep \(t\) as:

(18)#\[\varepsilon_{t} = |Q_i,t - Q_j,t|\]

where \(Q_i,t\) and \(Q_j,t\) are the sum of the outflow and inflow fluxes across the model boundaries at timestep \(t\), respectively. In a stable steady simulation, the ratio of inflows and outflows should converge toward a convergence constant c_{\varepsilon} equal to unity with increasing time:

(19)#\[\lim_{t\to \infty} \frac{\varepsilon_{t+1}}{\varepsilon^{\iota}_{t}} = c_{\varepsilon}\]

The combination of the convergence rate (or order) \(\iota\), and the convergence constant \(c_{\varepsilon}\) indicate:

  • linear convergence if \(\iota\) = 1 and \(c_{\varepsilon} \in ]0, 1[\)

  • slow sublinear convergence if \(\iota\) = 1 and \(c_{\varepsilon}\) = 1

  • fast superlinear convergence if \(\iota\) > 1 and \(c_{\varepsilon} \in ]0, 1]\)

  • divergence convergence if \(\iota\) = 1 and \(c_{\varepsilon}\) > 1; or \(\iota\) < 1

To determine the timestep at which a steady simulation can be considered to have reached a stable state, we want to observe when \(\iota\) = 1 and \(c_{\varepsilon}\) = 1 indicate sublinear convergence. That is, we look for the timestep \(t\) above which each additional timestep \(t+1\) only insignificantly improves the model precision (read more on the term insignificant in the below section). Thus, assuming that the model convergences in any form, we can set \(c_{\varepsilon}\) = 1 to compute \(\iota (t)\) as a function of \(\varepsilon_{t}\) and \(\varepsilon_{t+1}\):

(20)#\[\begin{align} \label{estimate_convergence} \frac{\varepsilon_{t+1}}{\varepsilon^{\iota(t)}_{t}} &=c_{\varepsilon} & \Leftrightarrow \\ \iota(t) &= \frac{1}{c_{\varepsilon}} \cdot \log_{\varepsilon_{t}\varepsilon_{t+1}} & \overbrace{\Longleftrightarrow }^{c_{\varepsilon} = 1}\\ \iota(t) &= \log_{\varepsilon_{t}\varepsilon_{t+1}} & \end{align}\]

This equation can be implemented in a function Python as follows:

import numpy as np
import pandas as pd


def calculate_convergence(Q_in, Q_out, conv_constant=1.):
    # calculate the error epsilon between two flux series
    epsilon = np.array(abs(Q_in - Q_out))
    # derive epsilon at t and t+1
    epsilon_t0 = epsilon[:-1]  # cut off last element
    epsilon_t1 = epsilon[1:]   # cut off element zero
    # return convergence rate as pandas DataFrame
    return  pd.DataFrame({"Convergence rate": np.emath.logn(epsilon_t0, epsilon_t1) / conv_constant })

Also this function is available in pythomac

from pythomac import calculate_convergence

To calculate \(\iota (t)\) (Python variable name: iota_t) with the above function, amend the example_flux_convergence.py Python script:

# example_flux_convergence.py

# ...
# add to header (alternatively copy-paste the above function into this script):
from pythomac import calculate_convergence

# calculate fluxes_df (see above code block)
fluxes_df = [...]

# calculate iota (t) with the calculate_convergence function
iota_t = calculate_convergence(
    fluxes_df["Fluxes Boundary 1"][1:],  # remove first zero-entry
    fluxes_df["Fluxes Boundary 2"][1:],  # remove first zero-entry
)

The resulting convergence rate \(\iota (t)\) is plotted in Fig. 199 for the steady 2d tutorial, with the modified printout periods of 50 seconds and a total simulation time of 10000 seconds.

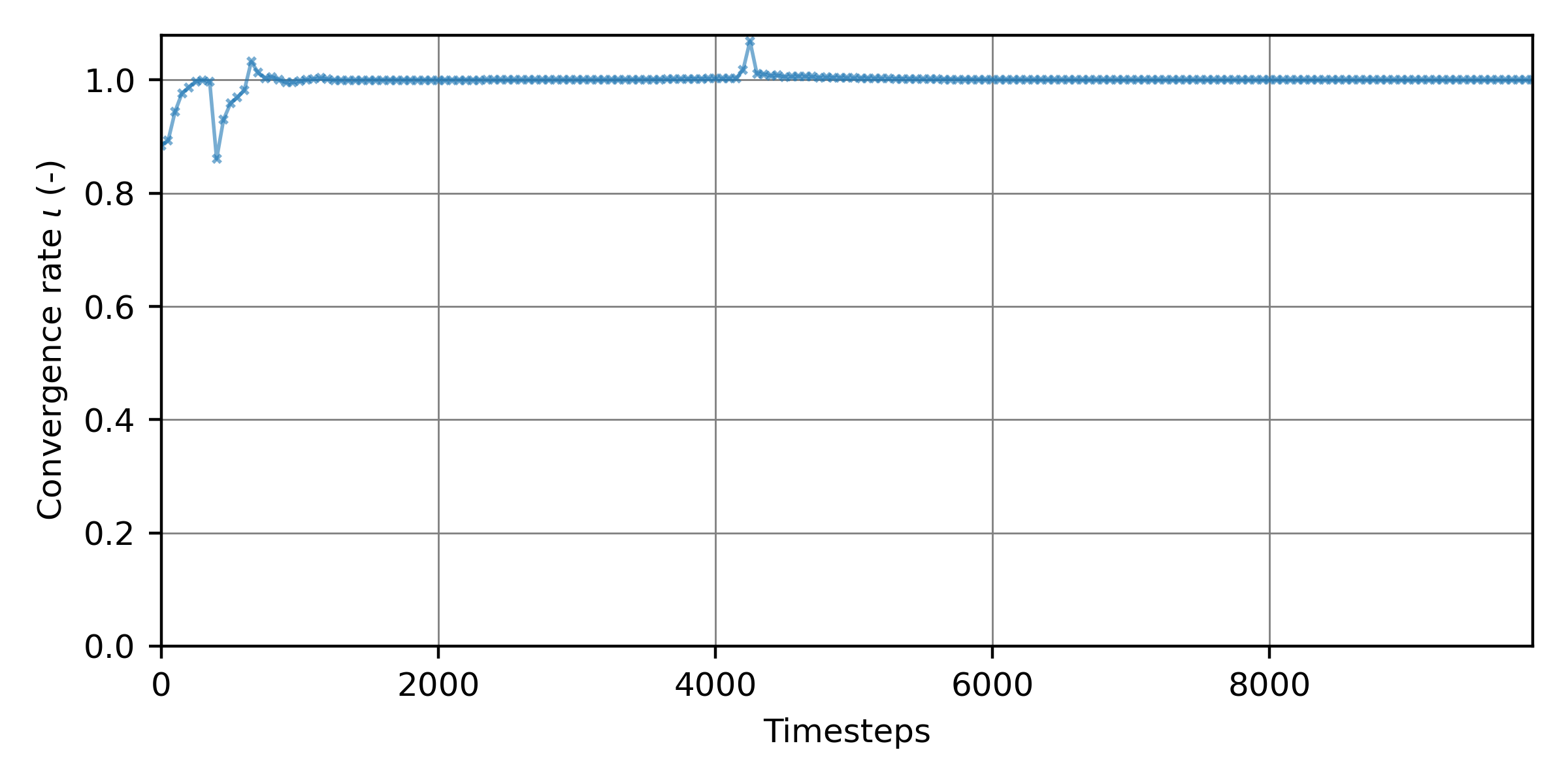
convergence rate fluxes telemac boundaries

Fig. 199 The convergence rate \(\iota\) as a function 10000 simulation timesteps of the steady 2d simulation.#

Derive Optimum Simulation Time#

To save computing time, we are interested in the timestep at which the inflow and outflow fluxes converged. The fluxes plotted in Fig. 198, and the convergence rate in Fig. 199 qualitatively suggest that the simulation was stable after approximately 6000 seconds (timesteps). The bumps in both figures after 4000 timesteps well indicate the “encounter” of the flux “waves” coming from the upstream and downstream boundaries (see the animation in the steady 2d tutorial). Only afterward, did convergence set in.

The definition of when convergence is reached (i.e., \(\iota\) being insignificant) can be subjective. Most modelers would agree that fluctuations of the convergence rate \(\iota\) of more than 0.1 to 0.01 are unacceptably high, but, depending on the problem considered, \(\iota\)-fluctuations in the order of 10\(^{-4}\) to 10\(^{-12}\) might be considered acceptable. To investigate at which simulation timestep a target convergence rate \(\iota_{tar}\) was achieved, we can analyze the vector of \(\iota (t)\) resulting from the above Equation. Specifically, we want to know after which timestep \(t\) the targeted convergence fluctuation \(\delta\iota_{tar}\) is not exceeded anymore. Note that \(\delta\iota (t)\) plotted in Fig. 199 achieved a possibly desired target convergence rate of \(\delta\iota_{tar}\) = 10\(^{-4}\) already after approximately 3000 timesteps, but \(\iota\) jumped up again after 4000 timesteps when the upstream “wave” rolled over the downstream boundary. Therefore, we want an algorithmic implementation that detects the last \(\iota_{t} - \iota_{t-1}\) > \(\delta\iota_{tar}\) in the vector of \(\iota (t)\). To this end, we can add to the above-started example_flux_convergence.py Python script the following code:

# example_flux_convergence.py

# ...

# calculate fluxes_df (see above code block)
fluxes_df = [...]

# calculate iota (t) with the calculate_convergence function
iota_t = [...]

# define a desired target convergence precision (delta iota_tar)
target_convergence_precision = 1.0E-6

# calculate the differences in the convergence rates
convergence_diff = np.diff(iota_t)

# find the index of the last element in the convergence differences that is larger than
#   the desired target convergence precision and add +1 (i.e., the first element being
#   permanently smaller than the desired precision)
idx = np.flatnonzero(abs(convergence_diff) > target_convergence_precision)[-1] + 1

# print the timestep at which the desired convergence was achieve to the console
printout_period_in_cas = 50  # the printout period defined in the cas file
print("The simulation converged after {0} simulation seconds ({1}th printout).".format(
        str(printout_period_in_cas * idx), str(idx)))

The simulation converged after 8050 simulation seconds (161th printout).

Bolster your code

The code for calculating the timestep at which a target convergence level was achieved is also implemented in the get_convergence_time() function in pythomac:

from pythomac import get_convergence_time

A full implementation with also a convenient way for retrieving the printout_period_in_cas variable can be found in this version of example_flux_convergence.py with documentation on https://pythomac.readthedocs.io.

Now that you know when your Telemac simulation converges satisfactorily, you can reduce the NUMBER OF TIME STEPS parameter in the .cas steering file, for example:

/ steady2d-conv.cas
TIME STEP : 1.
NUMBER OF TIME STEPS : 8050
GRAPHIC PRINTOUT PERIOD : 50
LISTING PRINTOUT PERIOD : 50

Troubleshoot Instabilities & Divergence#

If a steady simulation never reaches stability of fluxes or even flux divergence, make sure that all boundaries are robustly defined according to the spotlight section on boundary conditions, and have a look at the workflow in the next section on mass conservation.

Contents